QAOA
Similar to VQE, we also have two QAOA modes: a single-instance mode, and a graph partitioning mode. The single-instance mode can be used to find a solution to a single graph-based or QUBO-based optimization problem. The graph partitioning mode is a bit more specialized, focusing more on solving larger, less tractable problems through a partitioning approach. We will provide examples to demonstrate each mode and possible input in this section.
Single-instance QAOA
A QAOA constructor expects, obviously, a problem. As we will show in the examples, the form of input triggers a different
execution pathway under the hood. However, there are some common arguments that one must pay attention to.
A user has the ability to choose the initial state of the quantum system before the optimization. By default
(when the argument initial_state = "Recommended" is passed), a problem-specific initial state would be chosen.
Other accepted values are "Zero", "Ones, and "Superposition".
In addition, a user can determine how many layers of the QAOA ansatz to apply.
initial_state variable after initializing a QAOA object to determine
the resolved initial state.Finally, the solution of the QAOA problem can be accessed through the solution variable, which, based on the problem
at hand, would have different formats. For a graph problem, it will contain a set of node IDs that correspond to one
of the partitions of the solution. For QUBO optimization, it will return the solution bitstring as a list of 1’s and 0’s.
Graph Problems
Divi includes built-in support for several common graph-based optimization problems whose cost hamiltonians are available through Pennylane’s qaoa module. You can specify these using the graph_problem parameter when initializing a QAOA-based program. They are available through a GraphProblem enum.
| Problem | Description |
|---|---|
MAX_CLIQUE |
Finds the largest complete subgraph where every node is connected to every other. |
MAX_INDEPENDENT_SET |
Finds the largest set of vertices with no edges between them. |
MAX_WEIGHT_CYCLE |
Identifies a cycle with the maximum total edge weight in a weighted graph. |
MAXCUT |
Divides a graph into two subsets to maximize the sum of edge weights between them. |
MIN_VERTEX_COVER |
Finds the smallest set of vertices such that every edge is incident to at least one selected vertex. |
For all problems with the exception of Max-Cut, the constrained version of the Hamiltonian is available by passing the
keyword argument is_constrained=True to the constructor. Refer to the Pennylane documentation for more details.
The following is an example for finding the max-clique of the bull graph:
import networkx as nx
from divi.backends import ParallelSimulator
from divi.qprog import QAOA, GraphProblem
from divi.qprog.optimizers import ScipyMethod, ScipyOptimizer
G = nx.bull_graph()
qaoa_problem = QAOA(
problem=G,
graph_problem=GraphProblem.MAX_CLIQUE,
n_layers=2,
optimizer=ScipyOptimizer(method=ScipyMethod.NELDER_MEAD),
max_iterations=10,
is_constrained=True,
backend=ParallelSimulator(),
)
qaoa_problem.run()
qaoa_problem.compute_final_solution()
losses = qaoa_problem.losses[-1]
print(f"Minimum Energy Achieved: {min(losses.values()):.4f}")
print(f"Total circuits: {qaoa_problem.total_circuit_count}")
print(f"Classical solution:{nx.algorithms.approximation.max_clique(G)}")
print(f"Quantum Solution: {set(qaoa_problem.solution)}")
qaoa_problem.draw_solution()As you can see, Divi provides a visualization function after computing the solution. Running the code above will generate the following plot:
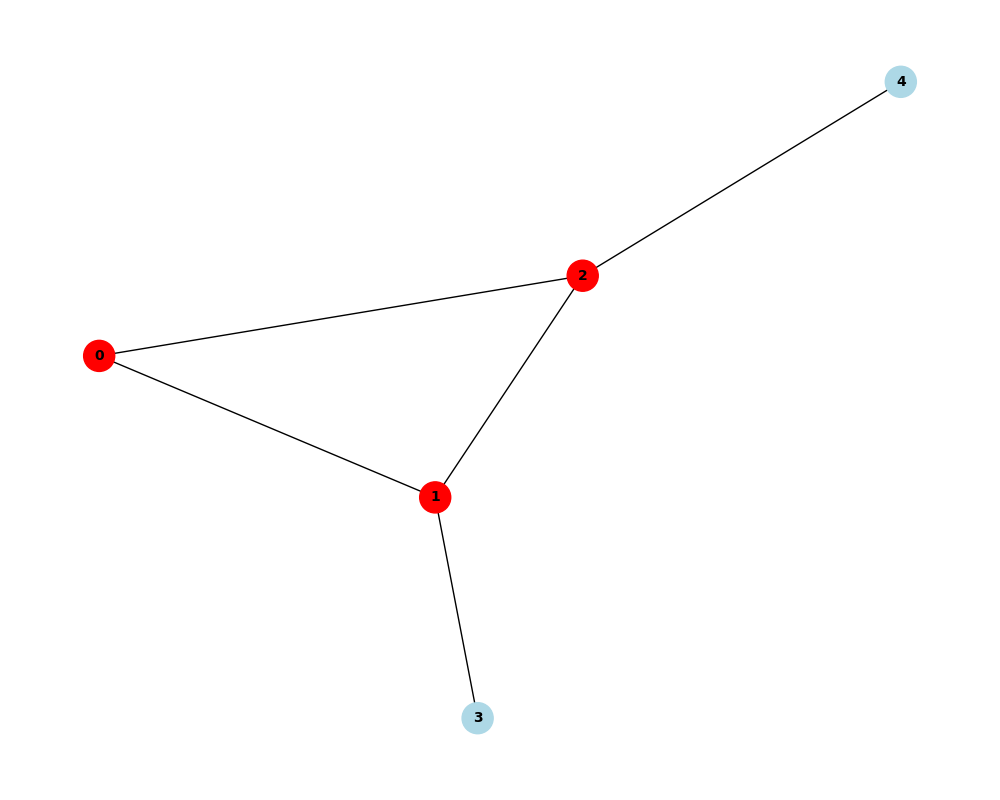
QAOA Max-Clique Solution on the Bull Graph
The solution can also be accessed through the solution property, which would generate the following list of node IDs corresponding to the Max-Clique:
>>> qaoa_problem.solution
[0, 1, 2]QUBO-based Problems
Divi’s QAOA solver can, instead of using a graph input, also take a (Quadratic Unconstrained Binary Optimization) QUBO formulated problem. There are only a few differences in the code to do so. Divi currently supports two methods of formulating the QUBO problem. The first, and the most straightforward, is to pass a numpy array or a scipy.sparse array. The second is using the qiskit-optimization library to create QuadraticPrograms.
In contrast to graph-based QAOA instances, the solution format for QUBO-based QAOA instances is a binary numpy array representing the value for each variable in the original QUBO.
qiskit-optimization is already included as a dependency of Divi, so have at it!Numpy Array-based Input
For illustration purposes, we use D-Wave’s dimod
to generate a random QUBO.
import dimod # For generating the problem
from divi.backends import QoroService
from divi.qprog import QAOA
from divi.qprog.optimizers import ScipyMethod, ScipyOptimizer
q_service = QoroService(QORO_API_KEY, shots=10000)
bqm = dimod.generators.randint(5, vartype="BINARY", low=-10, high=10, seed=1997)
qubo_array = bqm.to_numpy_matrix()
qaoa_problem = QAOA(
problem=qubo_array,
n_layers=2,
optimizer=ScipyOptimizer(method=ScipyMethod.L_BFGS_B),
max_iterations=5,
backend=q_service,
)
qaoa_problem.run()
qaoa_problem.compute_final_solution()
sol = qaoa_problem.solutionQiskit’s Quadratic Program
from qiskit_optimization import QuadraticProgram
from divi.backends import QoroService
from divi.qprog import QAOA
from divi.qprog.optimizers import ScipyMethod, ScipyOptimizer
q_service = QoroService(QORO_API_KEY, shots=10000)
qp = QuadraticProgram()
qp.binary_var("w")
qp.binary_var("x")
qp.binary_var("y")
qp.integer_var(lowerbound=0, upperbound=7, name="z")
qp.minimize(linear={"x": -3, "y": 2, "z": -1, "w": 10})
qaoa_problem = QAOA(
qp,
n_layers=2,
optimizer=ScipyOptimizer(method=ScipyMethod.COBYLA),
max_iterations=10,
backend=q_service,
)
qaoa_problem.run()
qaoa_problem.compute_final_solution()
sol = qaoa_problem.solution
# The binary mask as is might be useless when importing a QuadraticProgram
# You can evaluate the energy of the solution sample using:
print(qaoa_problem.problem.objective.evaluate(sol))
# And you can also translate it to the QuadraticProgram's variables using:
print(qaoa_problem._qp_converter.interpret(sol))Graph-Partitioning QAOA
This example demonstrates how to use Divi’s GraphPartitioningQAOA class to solve a MaxCut problem on large graphs. Instead of executing a single large QAOA circuit, the graph is partitioned into smaller subgraphs (clusters), and individual QAOA instances are executed in parallel across these subgraphs, before aggregating the results, in a divide-and-conquer manner.
This enables scalable quantum optimization, even for graphs that exceed the size limits of a single quantum backend.
Configuring the Partitioning
The partitioning strategy is configured using the PartitioningConfig class, which offers the following options:
-
max_n_nodes_per_cluster: This specifies the maximum number of nodes allowed in each subgraph or cluster. This is crucial for ensuring that each subproblem fits within the constraints of a single quantum backend. -
minimum_n_clusters: This parameter sets the minimum number of clusters to be created. -
partitioning_algorithm: A parameter that determines the algorithm used to partition the graph. The available options are:spectral: This refers to spectral clustering 1, an algorithm that uses the eigenvectors of the graph’s Laplacian matrix to partition the vertices. It’s known for producing high-quality partitions by minimizing the number of edges cut between the subgraphs. However, it might lead to unevenly sized partitions, based on the input graph.metis: Employs the popular METIS program 2 throughpy-metis. This algorithm generally generates more evenly sized partitions compared to spectral clustering.kernighan_linIteratively applies the classical Kernighan-Lin 3 bipartitioning algorithm until the desired number of clusters is achieved.
At least one of max_n_nodes_per_cluster and minimum_n_clusters must be provided to the class.
In case both are provided, the partitioning logic would first attempt creating the minimum number of desired partitions
first, before breaking down any oversized partitions further to meet the constraint on the number of nodes.
Code Example
from divi.qprog import GraphPartitioningQAOA, GraphProblem, PartitioningConfig
from divi.qprog.optimizers import Optimizer
from divi import QoroService
q_service = QoroService(QORO_API_KEY)
def analyze_results(quantum_solution, classical_cut_size):
cut_edges = 0
for u, v in graph.edges():
if (u in quantum_solution) != (v in quantum_solution):
cut_edges += 1
print(
f"Quantum Cut Size to Classical Cut Size Ratio = {cut_edges / classical_cut_size}"
)
graph = # A NetworkX graph
config = PartitioningConfig(max_n_nodes_per_cluster=4, partitioning_algorithm="metis")
qaoa_batch = GraphPartitioningQAOA(
graph_problem=GraphProblem.MAXCUT,
graph=graph,
n_layers=2,
partitioning_config=config,
optimizer=Optimizer.MONTE_CARLO,
max_iterations=5,
backend=q_service,
)
qaoa_batch.create_programs()
qaoa_batch.run().join()
qaoa_batch.compute_final_solutions()
quantum_solution = qaoa_batch.aggregate_results()
print(f"Total circuits: {qaoa_batch.total_circuit_count}")
analyze_results(quantum_solution, classical_cut_size)What’s Happening?
| Step | Description |
|---|---|
partitioning_config=config |
The graph is partitioned into a minimum of 4 subgraphs using the METIS algorithm. |
optimizer=MONTE_CARLO |
A lightweight Monte Carlo optimizer is used to minimize circuit evaluation cost. |
create_programs() |
Initializes a batch of QAOA programs, each solving a cluster of the original graph. |
run().join() |
Executes all generated circuits — possibly in parallel across multiple quantum backends and waits until all programs join. |
compute_final_solutions() |
Optimized bitstrings are retrieved for each cluster. |
aggregate_results() |
The final MaxCut solution is formed by combining cluster-wise results. |
If you are to inspect programs property of some GraphPartitioningQAOA instance, you would see a dictionary that looks like this, where the keys are tuples of the form (Partition ID, Partition Size), and the values are the individual QAOA instances that will optimize for the separate partitions:
{('A', 8): <divi.qprog._qaoa.QAOA object at 0x7622e9de2d90>,
('B', 8): <divi.qprog._qaoa.QAOA object at 0x7622ecbb8150>,
('C', 7): <divi.qprog._qaoa.QAOA object at 0x7622e9e48f90>,
('D', 7): <divi.qprog._qaoa.QAOA object at 0x762328767290>}The partitions can also be visualized through the function draw_partitions, whose output for the batch of QAOA programs above would produce this plot:
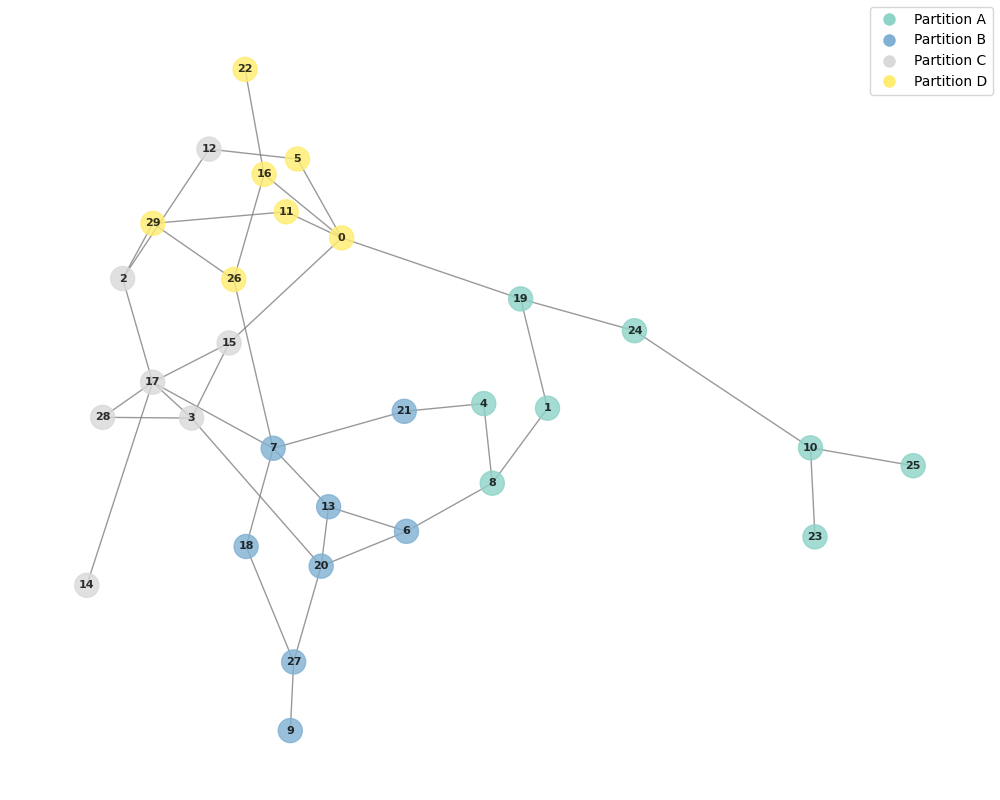
Generated Partitions for a 30-Node Graph with Max Nodes set to 10
QUBO-Partitioning QAOA
In addition to graphs, we also support partitioning capabilites for QUBOs, building our tool around D-wave’s hybrid library. The following is an example of how you can use their decomposers and composer classes in Divi.
from functools import partial
import dimod
import hybrid
import numpy as np
from divi.parallel_simulator import ParallelSimulator
from divi.qprog import QUBOPartitioningQAOA
from divi.qprog.optimizers import MonteCarloOptimizer
if __name__ == "__main__":
bqm: dimod.BinaryQuadraticModel = dimod.generators.gnp_random_bqm(
25,
p=0.5,
vartype="BINARY",
random_state=1997,
bias_generator=partial(np.random.default_rng().uniform, -5, 5),
)
optim = MonteCarloOptimizer(n_param_sets=10, n_best_sets=3)
qubo_partition = QUBOPartitioningQAOA(
qubo=bqm.to_numpy_matrix(),
decomposer=hybrid.EnergyImpactDecomposer(size=5),
composer=hybrid.SplatComposer(),
n_layers=2,
optimizer=optim,
max_iterations=10,
backend=ParallelSimulator(),
)
qubo_partition.create_programs()
qubo_partition.run().join()
print(f"Total circuits: {qubo_partition.total_circuit_count}")
quantum_solution, quantum_energy = qubo_partition.aggregate_results()
best_classical_bitstring, best_classical_energy, _ = (
dimod.ExactSolver().sample(bqm).lowest().record[0]
)
print(f"Classical Solution: {best_classical_bitstring}")
print(f"Classical Energy: {best_classical_energy:.9f}")
print(f"Quantum Solution: {quantum_solution}")
print(f"Quantum Energy: {quantum_energy:.9f}")Why Partition?
Quantum hardware is limited in the number of qubits and circuit depth. For large graphs:
- Full QAOA is intractable.
- Partitioned QAOA trades global optimality for scalability and parallel execution.
- It enables fast, approximate solutions using many small quantum jobs rather than one large one.
-
Fiedler, M. (1973). Algebraic connectivity of graphs. Czechoslovak Mathematical Journal, 23(2), 298-305. ↩︎
-
Karypis, G., & Kumar, V. (1997). METIS: A software package for partitioning unstructured graphs, partitioning meshes, and computing fill-reducing orderings of sparse matrices. Department of Computer Science and Engineering, University of Minnesota. ↩︎
-
Kernighan, B. W., & Lin, S. (1970). An efficient heuristic procedure for partitioning graphs. The Bell System Technical Journal, 49(2), 291-307. ↩︎